АРИФМЕТИКА
Предмет арифметики
Арифметика — это наука о числах. Название “арифметика” происходит от греческого слова “аритмбс” (по другому произношению “арнфмбс”), что означает “число”. В арифметике изучаются простейшие свойства чисел и правила вычислений. Более глубокие свойства чисел изучаются в теории чисел.
Целые (натуральные) числа
Первые представления о числе приобретались людьми с незапамятных времен. Они возникли из счета людей, животных, плодов, различных изделий человека н т. п. Результатом счета являются числа один, два, три и т. д. Эти числа называются натуральными. В арифметике их называют также целыми числами (наименование “целое число” имеет в математике и более широкий смысл.
Понятие о натуральном числе является одним из простейших понятий. Его можно пояснить лишь на примерах*).
Ряд целых чисел
1. 2, 3. 4, 5, ... продолжается бесконечно; он называется натуральным рядом.
Границы счета
На ранних ступенях развития общества люди почти не умели считать. Они различали совокупности двух и трех предметов; всякая совокупность, содержащая большее число предметов, объединялась в понятии “много”. Это был еще не счет, а лишь его зародыш.
Впоследствии способность различать одну от другой небольшие совокупности развивалась; возникли слова для обозначений понятий “четыре”, “пять”, “шесть”, “семь”.
С усложнением хозяйственной деятельности людей понадобилось вести счет в более обширных пределах. Для этого человек пользовался окружавшими его предметами как инструментами счета: он делал зарубки на палках и на деревьях, завязывал узлы на веревках, складывал камешки в кучки и т. п.
Евклид (III в. до н. ”.) определял число (натуральное) как “множество. составленное из единиц.: такого рода определения можно найти я во многих нынешних учебниках
От счета с помощью камешков ведут свое начало различные усовершенствованные инструменты. как. например, русские счеты, китайские счеты “сван-пан”
ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Особо важную роль играл природный инструмент человека — его пальцы. Этот инструмент не мог длительно хранить результат счета, но зато всегда был налицо и отличался большой подвижностью. Язык первобытного человека был беден; жесты возмещали недостаток слов, и числа, для которых еще не было названий, “показывались” на пальцах (мы тоже прибегаем к показу чисел на пальцах, когда объясняемся с человеком, не знающим нашего языка). Естественно, что вновь возникавшие названия “больших” чисел часто строились на основе числа 10—по количеству пальцев на руках; у некоторых народов возникли также названия чисел на основе числа 5—по количеству пальцев на одной руке или на основе числа 20 — по количеству пальцев на руках и на ногах.
На первых порах расширение запаса чисел происходило медленно. Сначала люди овладевали счетом в пределах нескольких первых десятков и лишь позднее дошли до сотни. У многих народов число 40 долгое время было пределом счета и названием неопределенно большого количества. В русском языке слово “сороконожка” имеет смысл
“многоножка”; выражение “сорок сороков” означало в старину число, превосходящее всякое воображение. Тот же смысл имеет слово “сорок” в ряде русских пословиц и поговорок (“и один глаз, да зорок, не надо и сорок”, “сидела сорок лет, высидела сорок реп” и др.)На следующей ступени счет достигает нового предела: десяти десятков, и создается название для числа 100. Вместе с тем слово “сто” приобретает смысл неопределенно большого числа *). Такой смысл оно имеет, например, в загадке: стоит поп низок, на нем сто ризок (капуста). Такой же смысл потом приобретают последовательно числа тысяча, десять тысяч (в старину это число называлось “тьма”), миллион. , .
Десятичная система счисления
В русском языке, а также в языках других народов названия всех чисел до миллиона составляются из 37 слов, обозначающих числа I, 2, 3, 4, 5, 6, 7. 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000 (например, девятьсот восемнадцать тысяч семьсот сорок два). В свою очередь названия этих 37 чисел, как правило, образованы из названий чисел первого десятка (I, 2, 3, 4, 5, 6, 7, 8, 9) и чисел 10, 100, 1000 (например, Г8=восемь на десять, 30= тридесять, т. е. три десятка, 300=триста, т. ё. три сотни). В основе этого словообразования лежит число 10, и потому наша система наименований называется десятичной системой счисления. Исключительная роль, принадлежащая числу 10, объясняется тем, что на руках у нас 10 пальцев (см. § 3).
Из упомянутого правила в разных языках имеются различные исключения, объясняющиеся историческими особенностями развития счета. В русском языке, единственным исключением является наименование “сорок”. (прежде наряду с ним употреблялось и слово “четыре-десят”). Это исключение можно связать с тем, что число 40 играло некогда особую роль, означая неопределенно большое количество. В тюркских языках (азербайджанском, узбекском, туркменском, казахском, татарском, турецком и др.) исключение составляют наименования чисел 20, 30, 40, 50, тогда как названия чисел 60, 70, 80, 90 образованы из наименований для 6, 7, 8, 9. В монгольском языке, наоборот, наименования чисел 20, 30, 40, 50 следуют общему правилу, а наименования 60, 70, 80, 90 составляют исключение
Развитие понятия числа
При счете отдельных предметов единица есть наименьшее число; делить ее на доли не нужно, а часто и нельзя (при счете камней прибавление к двум камням половины третьего дает 3 камня.
Довольно поздно к семье чисел присоединился нуль. Первоначально слово “нуль” означало отсутствие числа. Действительно, если, например, от 3 отнять 3, то не остается ничего. Основания для того, чтобы это “ничего” считать числом, появились лишь в связи с рассмотрением отрицательных чисел.
Цифры
Цифра — это письменный знак, изображающий число. В древнейшие времена числа обозначались прямолинейными пометками (“палочками”): одна палочка изображала единицу, две палочки—двойку и т. д. Этот способ записи происходит от зарубок. Он и поныне сохранился в “римских цифрах” для изображения чисел I, 2, 3.
Для изображения сколько-нибудь больших чисел этот способ был непригоден. Поэтому появились особые знаки для числа 10, а у некоторых народов и для числа 5 (в соответствии с пятеричным счетом, по числу пальцев на одной руке). Позднее были созданы знаки для больших чисел. Знаки
эти у разных народов имели разную форму и с течением времени видоизменялись. Различны были и системы нумерации, т.е. способы соединения цифр для изображения больших чисел. Однако в большинстве систем нумерации основное значение имеет десятичная основа в соответствии с преобладанием десятичной системы счисления.Системы нумерации некоторых народов
1. Древнегреческая нумерация. В древнейшее время в Греции была распространена так называемая аттическая нумерация. Числа I, 2, 3, 4 обозначались черточками I, II, III, IIII. Г", Числа в пределах первого десятка тысяч записывались так:

и
т. д.В III в. до н. э. аттическая нумерация была вытеснена так называемой ионийской системой.


и т. д.
Шестидесятеричная система возникла позднее десятичной, ибо числа до 60 записываются в ней по десятичному принципу. Но до сих пор неизвестно, когда и как возникла у вавилонян шестидесятеричная система. На этот счет строилось много гипотез, но ни одна пока не доказана.
Шестидесятеричная запись целых чисел не получила распространения за пределами ассиро-вавилонского царства, но шестидесятеричные дроби проникли далеко за эти пределы: в страны Ближнего Востока, Средней Азии, в Северную Африку и Западную Европу. Они широко применялись, особенно в астрономии, вплоть до изобретения десятичных дробей, т. е. до начала XVII в. Следы шестидесятеричных дробей сохраняются и поныне в делении углового и дугового градусов (а также часа) на 60 минут и минуты на 60 секунд.
5. Римские цифры. Древние римляне пользовались нумерацией, которая сохраняется до настоящего времени под именем римской нумерации. Мы пользуемся ею для обозначения юбилейных дат, для наименования съездив и конференций, для нумерации глав в книгах, строф в стихотворениях и т. д.
В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян (латинском) никаких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (весьма вероятно—у этрусков).
Все целые числа (до 5000) записываются с помощью повторения вышеприведенных цифр. При этом, если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае она не может повторяться), то меньшая вычитается из большей. Например, VI == 6, т. е. 5-1> IV = 4, т. е.
Первые 12 чисел записываются в римских цифрах так:

Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Тем не менее римская нумерация преобладала в Италии до XIII в., а в других странах Западной Европы — до XVI в.
6. Индийская поместная нумерация. В различных областях Индии существовали разнообразные системы нумерации. Одна из них распространилась по всему миру и в настоящее время является общепринятой. В ней цифры имели вид начальных букв соответствующих числительных на древнеиндийском языке — санскрите (алфавит “девангари”).
Первоначально этими знаками представлялись числа 1, 2, 3,... ..„ 9, 10, 20, 30, .... 90, 100, 1000; с их помощью записывались другие числа. Впоследствии был введен особый знак (жирная точка, кружок) для указания пустующего разряда; знаки для чисел, больших 9, вышли из употребления, и нумерация “девангари” превратилась в десятичную поместную систему. Как и когда совершился этот переход—до сих пор неизвестно. К середине VIII в. позиционная система нумерации получает в Индии широкое применение. Примерно в это время она проникает и в другие страны (Индокитай, Китай, Тибет, на территорию наших среднеазиатских республик, в Иран и др.). Решающую роль в распространении индийской нумерации в арабских странах сыграло руководство, составленное в начале IX в. Мухаммедом из Хорезма (ныне Хорезмская область Узбекской ССР)
. Оно было переведенов Западной Европе на латинский язык в XII в. В XIII в; индийская нумерация получает Преобладание в Италии. В других странах Западной Европы она утверждается в XVI в. Европейцы, заимствовавшие индийскую нумерацию от арабов, называли ее арабской. Это исторически неправильное название удерживается и поныне.
Из арабского языка заимствовано и слово “шифра” (по-арабски “сыфр”), означающее буквально “пустое место” (перевод санскритского слова “сунья”, имеющего тот же смысл)
Это слово первоначально употреблялось для наименования знака пустующего разряда и этот смысл сохраняло еще в XVIII в., хотя уже в XV в. появился латинский термин <нуль”.
Форма индийских цифр претерпевала многообразные изменения. Та форма, в которой мы их пишем, установилась в XVI в.
Наименования больших чисел
Для удобства чтения и запоминания больших чисел цифры их разбивают на так называемые классы: справа отделяют три цифры (первый класс), затем еще три (второй класс) и т. д. Последний класс может иметь три, две или одну цифру. Между классами обычно оставляется небольшой пробел. Например, число 35461298 записывают так: 35461298. Здесь 298 — первый класс, 461—второй, 35—третий. Каждая из цифр класса называется разрядом; счет разрядов также идет справа. Например, в первом классе 298 цифра 8 составляет первый разряд, 9— второй, 2— третий. В последнем классе может быть три, два разряда (в нашем примере: 5— первый разряд, 3— второй) или одия.
Первый класс дает число единиц, второй — тысяч, третий—миллионов; сообразно с этим число 35461298 читается: тридцать пять миллионов четыреста шестьдесят одна тысяча двести девяносто восемь. Поэтому говорят, .что единица, второго класса есть тысяча; единица третьего класса—миллион.
Единица четвертого класса называется миллиардом или, иначе, биллионом (1 миллиард = 1000 миллионов).
Единица пятого класса называется триллионом (1 .триллион == =1000 биллионов или 1000 миллиардов). Единицы шестого, седьмого, восьмого и т. д. классов (каждая в 1000 раз больше предшествующей) называются квадриллионом, квинтиллионом, секстиллионом, септиллионом и т. д.
Пример. 12 021 306 200 000 читается: двенадцать триллионов двадцать один миллиард триста шесть миллионов двести тысяч. в Западной Европе на латинский язык в XII в. В XIII в; индийская нумерация получает Преобладание в Италии. В других странах Западной Европы она утверждается в XVI в. Европейцы, заимствовавшие индийскую нумерацию от арабов, называли ее арабской. Это исторически неправильное название удерживается и поныне
.Из
арабского языка заимствовано и слово “шифра” (по-арабски “сыфр”), означающее буквально “пустое место” (перевод санскритского слова “сунья”, имеющего тот же смысл)Это слово первоначально употреблялось для наименования знака пустующего разряда и этот смысл сохраняло еще в XVIII в., хотя уже в XV в. появился латинский термин <нуль”.
Форма индийских цифр претерпевала многообразные изменения. Та форма, в которой мы их пишем, установилась в XVI в.
Наименования больших чисел
Для удобства чтения и запоминания больших чисел цифры их разбивают на так называемые классы: справа отделяют три цифры (первый класс), затем еще три (второй класс) и т. д. Последний класс может иметь три, две или одну цифру. Между классами обычно оставляется небольшой пробел. Например, число 35461298 записывают так: 35461298. Здесь 298 — первый класс, 461—второй, 35—третий. Каждая из цифр класса называется разрядом; счет разрядов также идет справа. Например, в первом классе 298 цифра 8 составляет первый разряд, 9— второй, 2— третий. В последнем классе может быть три, два разряда (в нашем примере: 5— первый разряд, 3— второй) или одия.
Первый класс дает число единиц, второй — тысяч, третий—миллионов; сообразно с этим число 35461298 читается: тридцать пять миллионов четыреста шестьдесят одна тысяча двести девяносто восемь. Поэтому говорят, .что единица, второго класса есть тысяча; единица третьего класса—миллион.
Единица четвертого класса называется миллиардом или, иначе, биллионом (1 миллиард = 1000 миллионов).
Единица пятого класса называется триллионом (1 .триллион == =1000 биллионов или 1000 миллиардов). Единицы шестого, седьмого, восьмого и т. д. классов (каждая в 1000 раз больше предшествующей) называются квадриллионом, квинтиллионом, секстиллионом, септиллионом и т. д.
П р и ме р. 12 021 306 200 000 читается: двенадцать триллионов двадцать один миллиард триста шесть миллионов двести тысяч.

Способ записи чисел называют системой счисления, или нумерацией. А если в записи числа значение каждого символа зависит от того места, которое он занимает, то система счисления называется позиционной.
Мы пользуемся десятичной позиционной системой счисления. Слово “десятичная” означает, что мы ведем счет десятками и степенями десятков. У позиционной системы счисления очень много достоинств - с помощью небольшого набора символов (цифр) можно записывать сколь угодно большие числа. В позиционной системе счисления очень удобно выполнять арифметические действия - если знать, как складываются или умножаются однозначные числа, то легко научиться выполнять эти действия и с любыми многозначными числами. Именно поэтому вы все в начальной школе учили наизусть таблицы сложения и умножения.
Но позиционные системы счисления возникли не сразу -у многих народов долгое время использовались другие способы записи чисел. Очень часто для такой записи применялись буквы, снабженные какими-то дополнительными значками. Так записывали числа в древней Греции, такой же способ записи использовали славянские народы.
А вот в древнем Риме для записи чисел использовались специальные знаки, но римская система записи чисел не была позиционной и выполнять в ней арифметические действия было очень неудобно.
По всей видимости, первая позиционная система счисления возникла в древнем Вавилоне. Государство Вавилон образовалось в результате объединения шумерского и аккадского государств. У каждого из этих государств были свои весовые и денежные единицы. У шумерийцев основной весовой единицей была “мина” (приблизительно из килограмма). Денежной единицей служила мина , серебра. У аккадцев единица веса-“шекель” - была примерно в 60 раз меньше, чем мина. После слияния государств использовались обе единицы веса - и мина, и шекель. А через некоторое время возникла новая единица веса “талант” - он был в 60 раз тяжелее мины. На основе
, расчетов с этими единицами и возникла вавилонская система счисления - позиционная шестидесятиричная.Как вы, наверное, уже знаете, жители древнего Вавилона писали палочками на плитках из мягкой глины. Потом эти плитки обжигали в печи, и получались прочные , “документы". Многие из них сохранились почти 4 тысячи лет, и при раскопках в наше время археологи нашли целые архивы, содержащие тысячи глиняных табличек.
Глиняные таблички были очень прочными, но изображать на них сложные символы было неудобно, поэтому вавилонские письмена состояли, в основном, из комбинаций узких вертикальных или горизонтальных клинышков.
Числа первого десятка изображались вертикальными клинышками, а для изображения числа 10 был особый значок - широкий горизонтальный клинышек.
Первоначально мины обозначались значками большего размера, чем шекели. Позже все единицы стали записывать значками одинаковых размеров, и только положение значка указывало, какие единицы он изображал.
Когда появились отвлеченные числа, то есть числа, не связанные ни с какими единицами измерения, их стали записывать по тем же правилам.
Наша современная система счисления возникла в Индии в VI веке. Но сначала в ней было только 9 цифр - вместо нуля оставляли пустое место, а позже стали ставить точку или маленький кружок. Только в IX веке появился специальный знак для нуля.
Из Индии эта система счисления была заимствована арабами, а уже они в Х-ХШ веках познакомили с ней европейцев. Новые цифры в Европе называли арабскими. Однако до XVIII века в официальных бумагах разрешалось ставить только римские цифры. В России десятичная позиционная счисления стала широко использоваться в XVI веке.
Понятно, что в основу позиционной системы счисления можно положить любое натуральное число, например, 7. Для такой системы счисления потребуется 7 цифр, например, 0, 1, 2, 3, 4, 5 и 6. Если мы хотим число, записанное в десятичной системе, переписать в семиричную (то есть систему счисления с основанием 7), мы должны разделить его на 7, тогда остаток равен цифре единиц новой записи. Затем надо частное, полученное при первом делении, снова разделить на 7 - остаток будет равен числу полных семерок, и так далее.

Операции с числами в семиричной системе выполняются по тем же правилам, что и в десятичной, только с другими таблицами сложения и умножения.
Например, сложим два числа в семиричной системе счисления:


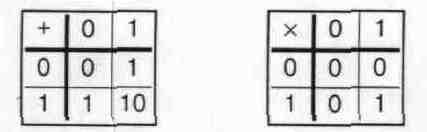
Особенно просто выполняются арифметические операции в двоичной системе счисления. Как и в любой позиционной системе счисления, для этого достаточно помнить лишь таблицы сложения и умножения, которые в этом случае выглядят совсем просто:
Следующие примеры показывают, как пользоваться этими таблицами:

Однако, при создании электронно-вычислительной техники оказалось, что арифметические действия удобнее всего выполнять именно в двоичной системе счисления. Это связано с тем, что с каждой цифрой должно быть связано определенное состояние элементарной “ячейки” компьютера. Поскольку в двоичной системе счисления цифр всего две, то можно использовать ячейки всего с двумя состояниями. Компьютеры с такими ячейками сконструировать намного проще, и работают они значительно надежнее.
Подробнее о различных системах счисления можно прочитать в книге С. В. Фомина “Системы счисления", издательство “Наука”, серия “Популярные лекции по математике”, выпуск 40.
Системы счисления.
В этом разделе мы начнем изучать понятие системы счисления. Зачем нам это? Дело в том, что позже нам понадобится довольно широко пользоваться разными системами - переводить числа из одной в другую или работать с несколькими системами счисления одновременно
. Поэтому нам необходимо заранее ознакомиться с понятием системы счисления, чтобы в дальнейшем подойти подготовленными к этому вопросу.- Система счисления - что она из себя представляет? На практике существует некое стандартное определение системы счисления
Система счисления -это совокупность приемов и правил изображения чисел цифровыми знаками.
- Если проще - то система счисления это то, каким образом изображается конкретное число. Также можно разделить системы счисления на позиционные и непозиционные, где:
- Позиционные -
это те системы счисления, в которых значение символа зависит от его места в ряду цифр, изображающих число. Примером таких систем может служить десятичная система, которой мы все с успехом пользуемся. Т.е. если разобрать число 564 согласно этому правилу, то получается, что 5 - это сотни, 6 - десятки, а 4 - единицы. Выходит, что каждая цифра соответствует своему разряду и зависит от своего места в ряду цифр. Эта зависимость особо становиться понятна, если предположить, что мы поменяли местами цифры 6 и 4. Четверка сразу же стала десятками, а 6-ка единицами.
- Непозиционные -
это системы счисления, числа в которых не зависят от своего местонахождения в ряду цифр и число изображается не цифрами, а специальными значками, которые отображают свое значение через сложение или вычитание друг друга. Примером такой системы может служить Римская. В этой системе можно определить следующее правило:
Каждый меньший знак, стоящий справа от большего, прибавляется к его значению, а слева - вычитается из него.
- Поясню на примере:
IV = V - I - Римское Число 4. Единица, стоящая слева от пятерки вычитается из нее, образует четыре.
XI = X + I - Римское Число 11. Единица, стоящая справа от десятки прибавляется к ней, образуя 11. - В общем, мы разобрались, что такое система счисления и какие виды систем бывают. Но это еще не все, что необходимо про них знать. На практике также существует такое понятие, как Основание системы счисления. Сразу скажу, что основание можно рассматривать только у позиционных систем, далее сами поймете почему.
- Так вот, что же такое Основание? Опять, существует стандартное определение:
Основание позиционной системы счисления- это количество знаков или символов, используемых в разрядах для изображения числа в данной системе счисления.
- Объясню проще.
Вот, например, возьмем нашу с вами, десятичную систему счисления. Сколько знаков в разрядах числа используется в ней для изображения числа? Десять. То есть это 10 цифр от 0 до 9. Я имею в виду, что кроме цифр 0-9 мы не пользуемся больше ничем - и этими десятью цифрами мы можем изобразить любое число. По определению выходит, что количество знаков или символов, используемых в разрядах для изображения числа в 10-чной системе счисления явл. 10. То есть основание десятичной системы - десять. Вот и все определение основания системы счисления.
В отличии от обычных чисел 0,1,2,3...9 (называемых 10-ой системой счислений по числу знаков) в вычислительной технике информация передается при помощи нулей и единиц т.е. кодируется. Такое кодирование называется двоичным кодированием, а цифры 0 и 1 битами. При двоичном кодировании каждому символу присваивается код последовательность из нулей и единиц. Каждому символу соответствует последовательность из 8-ми нулей и единиц. Такая последовательность называется словом или байтом. Всего существует 256 различных комбинаций
Например :
|
10-система |
2-система |
|
0 |
0 |
|
1 |
01 |
|
2 |
10 |
|
3 |
11 |
Для записи чисел в привычной 10-ой системе счисления используются знаки от 0 до 9. Так число 23 состоит из 2-х десятков и 3-х единиц, если эти знаки поменять между собой то получим другое число. Цифры десятичной записи числа это коэффициенты его представления в виде суммы степеней числа 10- основания системы счисления.
25076=2*104+5*103+0*102+7*101+6*100
самостоятельно : 341,89
Любое число можно представить как сумму степеней не только числа 10 но и любого другого натурального числа больше 1.
2710=1*24+1*23+0*22+1*21+1*20=110112
111010,12=1*25+1*24+1*23+0*22+1*21+0*20+1*2-1=58,510
Заполнить таблицу.
|
2-система |
8-система |
10-система |
|
010111,1 |
|
|
|
|
126,4 |
|
|
|
|
2683,1 |
|
|
284,3 |
|
|
1001,1 |
|
|